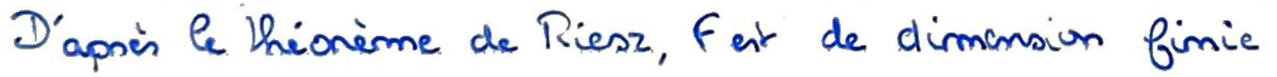Démonstration du théorème de Riesz
\((i)\implies(ii)\)

C'est un fermé borné d'un evn de dimension finie, donc un compact.

Démonstration du théorème de Riesz
\((ii)\implies(iii)\)

C'est immédiat par précompacité.

Démonstration du théorème de Riesz
\((iii)\implies(i)\)

On pose l'espace vectoriel engendré par le centre des boules \(\to\) dimension finie car nombre fini de boules.

Si \(F=E\), alors c'est ok.

Sinon, alors on applique le Lemme de Riesz pour avoir une absurdité (via distance \(=1\)).

Soit \(F\) un sous-espace vectoriel Fermé de \(\mathcal C([0,1])\) muni de la norme de la convergence uniforme.
On suppose que tous les éléments de \(F\) sont dans \(\mathcal C^1([0,1])\).
On sait qu'il existe \(C\gt 0\) tq $$\forall f\in F,\quad\lVert f^\prime\rVert_\infty\leqslant C\lVert f\rVert_\infty.$$
On en a déduit que la boule unité fermée de \(F\) (pour \(\lVert\cdot\rVert_\infty\)).
Que peut-on en conclure ?

\(F\) est de dimension finie d'après le Théorème de Riesz.